Edit

Model

神经网络中的前向和反向传播可以用一组操作来表示，比如卷积和池化。每个操作都需要一 些输入的tensors，并应用一个operator来生成输出的张量。 通过将每个运算符表示为一个节点，将每个张量表示为一条边，所有的运算就形成了一个计 算图。有了计算图，可以通过调度运算的执行和内存的智能分配/释放来进行速度和内存优 化。在 SINGA 中，用户只需要使 用Model API 定义神经网络模型，计算图则会在 C++后台自动构建和优化。

这样，一方面，用户使用Model API 按照 PyTorch 那样的命令式编程风格实现 网络。而与 PyTorch 在每次迭代中重新创建操作不同的是，SINGA 在第一次迭代后就会缓 冲操作，隐式地创建计算图（当该功能被启用时）。因此，另一方面，SINGA 的计算图与使 用声明式编程的库（如 TensorFlow）创建的计算图类似，因而它可以享受在图上进行的优 化。

样例

下面的代码说明了ModelAPI 的用法：

1. 将新模型实现为 Model 类的子类：

class CNN(model.Model):

    def __init__(self, num_classes=10, num_channels=1):
        super(CNN, self).__init__()
        self.conv1 = layer.Conv2d(num_channels, 20, 5, padding=0, activation="RELU")
        self.conv2 = layer.Conv2d(20, 50, 5, padding=0, activation="RELU")
        self.linear1 = layer.Linear(500)
        self.linear2 = layer.Linear(num_classes)
        self.pooling1 = layer.MaxPool2d(2, 2, padding=0)
        self.pooling2 = layer.MaxPool2d(2, 2, padding=0)
        self.relu = layer.ReLU()
        self.flatten = layer.Flatten()
        self.softmax_cross_entropy = layer.SoftMaxCrossEntropy()

    def forward(self, x):
        y = self.conv1(x)
        y = self.pooling1(y)
        y = self.conv2(y)
        y = self.pooling2(y)
        y = self.flatten(y)
        y = self.linear1(y)
        y = self.relu(y)
        y = self.linear2(y)
        return y

    def train_one_batch(self, x, y):
        out = self.forward(x)
        loss = self.softmax_cross_entropy(out, y)
        self.optimizer(loss)
        return out, loss

2. 创建 model、optimizer、device 等的实例。编译模型：

model = CNN()

# initialize optimizer and attach it to the model
sgd = opt.SGD(lr=0.005, momentum=0.9, weight_decay=1e-5)
model.set_optimizer(sgd)

# initialize device
dev = device.create_cuda_gpu()

# input and target placeholders for the model
tx = tensor.Tensor((batch_size, 1, IMG_SIZE, IMG_SIZE), dev, tensor.float32)
ty = tensor.Tensor((batch_size, num_classes), dev, tensor.int32)

# compile the model before training
model.compile([tx], is_train=True, use_graph=True, sequential=False)

3. 迭代训练：

for b in range(num_train_batch):
    # generate the next mini-batch
    x, y = ...

    # Copy the data into input tensors
    tx.copy_from_numpy(x)
    ty.copy_from_numpy(y)

    # Training with one batch
    out, loss = model(tx, ty)

这个例子的 Google Colab notebook 可以 在这里找 到。

更多例子：

• MLP
• CNN
• ResNet

实现

图的构建

SINGA 分三步构建计算图：

1. 将操作保存在缓冲区。
2. 分析操作的依赖性。
3. 根据依赖关系创建节点和边。

以 MLP 模型的 dense 层的矩阵乘法运算为例，该操作会 在MLP model的 前向函数中被调用：

class MLP(model.Model):

    def __init__(self, data_size=10, perceptron_size=100, num_classes=10):
        super(MLP, self).__init__()
        self.linear1 = layer.Linear(perceptron_size)
        ...

    def forward(self, inputs):
        y = self.linear1(inputs)
        ...

线性层由mutmul运算符组成，autograd通过 SWIG 调用 CPP 中提供的Mult函数来 实现matmul运算符。

# implementation of matmul()
singa.Mult(inputs, w)

At the backend, the Mult function is implemented by calling GEMV a CBLAS function. Instead of calling GEMV directly, Mult submits GEMV and the arguments to the device as follows, 在后端，Mult函数是通过调用GEMV一个 CBLAS 函数来实现的。但Mult没有直接调用GEMV，而是将GEMV和参数提交给设备，具体如下 。

// implementation of Mult()
C->device()->Exec(
    [a, A, b, B, CRef](Context *ctx) mutable {
        GEMV<DType, Lang>(a, A, B, b, &CRef, ctx);
    },
    read_blocks, {C->block()});

Device的Exec函数对函数及其参数进行缓冲。此外，它还拥有这个函数要读写的块的信 息（块是指张量的内存块）。

一旦Model.forward()被执行一次，所有的操作就会被Device缓冲。接下来，对所有操 作的读写信息进行分析，用来建立计算图。例如，如果一个块b被一个操作 O1 写入，之 后又被另一个操作 O2 读出，我们就会知道 O2 依赖于 O1 并且有一条从 A 到 B 的有向边 ，它代表了块b（或其张量）。之后我们就构建了一个有向无环图，如下图所示。该图会 构建一次。

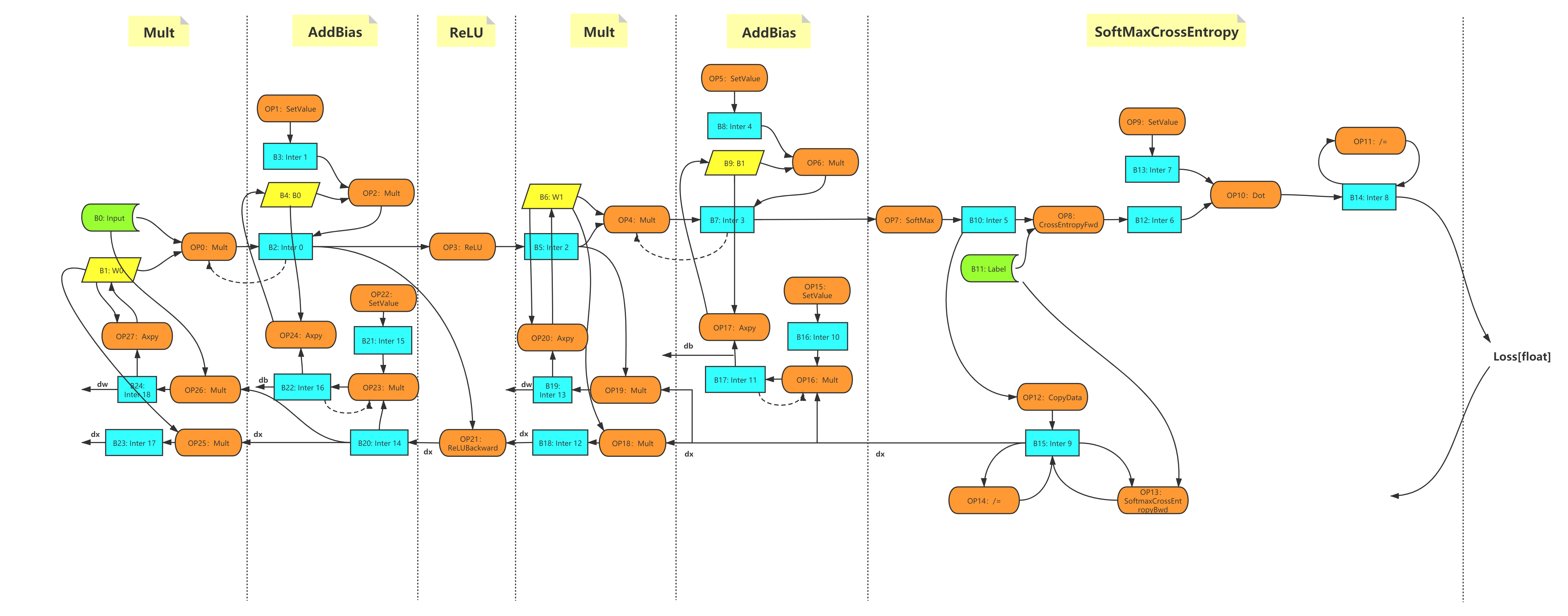
Figure 1 - MLP 例子的计算图

优化

目前，基于计算图进行了以下优化：

惰性分配 当创建张量/块时，设备不会立即为它们分配内存。相反，是在第一次访问块 时，才会分配内存。

自动回收 每个张量/块的参考计数是根据图计算出来的。在执行操作之前，参考计数是 读取这个块的操作次数。在执行过程中，一旦执行了一个操作，每一个输入块的参考数就会 减少 1，如果一个块的参考数达到了 0，就意味着这个块在剩下的操作中不会再被读取。因 此，它的内存可以被安全释放。此外，SINGA 还会跟踪图外的块的使用情况。如果一个块被 Python 代码使用（而不是被 autograd 操作符使用），它将不会被回收。

内存共享 SINGA 使用内存池，如CnMem来管理 CUDA 内存。有了自动回收和内存池，SINGA 就可以在张量之间共享内存。考虑两个操 作c=a+b和d=2xc。在执行第二个操作之前，根据惰性分配原则，应该分配 d 的内存。 假设a在其余操作中没有使用。根据自动回收，a的块将在第一次操作后被释放。因此 ，SINGA 会向 CUDA 流提交四个操作：加法、释放a、分配b和乘法。这样，内存池就可 以将a释放的内存与b共享，而不是要求 GPU 为b做真正的 malloc。

其他的优化技术，如来自编译器的优化技术，如常见的子表达式消除和不同 CUDA 流上的并 行化操作也可以应用。

新的操作符

autograd模块中定义的每个运算符都实现了两个功能：前向和反向，通过在后台调用运算 符来实现。如果要在autograd中添加一个新的运算符，需要在后台添加多个运算符。

以Conv2d运 算符为例，在 Python 端，根据设备类型，从后台调用运算符来实现前向和反向功能：

class _Conv2d(Operation):

    def forward(self, x, W, b=None):
        ......
        if training:
            if self.handle.bias_term:
                self.inputs = (x, W, b) # record x, W, b
            else:
                self.inputs = (x, W)

        if (type(self.handle) != singa.ConvHandle):
            return singa.GpuConvForward(x, W, b, self.handle)
        else:
            return singa.CpuConvForward(x, W, b, self.handle)

    def backward(self, dy):
        if (type(self.handle) != singa.ConvHandle):
            dx = singa.GpuConvBackwardx(dy, self.inputs[1], self.inputs[0],
                                        self.handle)
            dW = singa.GpuConvBackwardW(dy, self.inputs[0], self.inputs[1],
                                        self.handle)
            db = singa.GpuConvBackwardb(
                dy, self.inputs[2],
                self.handle) if self.handle.bias_term else None
        else:
            dx = singa.CpuConvBackwardx(dy, self.inputs[1], self.inputs[0],
                                        self.handle)
            dW = singa.CpuConvBackwardW(dy, self.inputs[0], self.inputs[1],
                                        self.handle)
            db = singa.CpuConvBackwardb(
                dy, self.inputs[2],
                self.handle) if self.handle.bias_term else None
        if db:
            return dx, dW, db
        else:
            return dx, dW

对于后台的每一个操作符，应按以下方式实现：

• 假设操作符是foo()，它的真正实现应该包装在另一个函数中，例 如_foo()。foo()将_foo和参数一起作为 lambda 函数传递给Device的Exec函 数进行缓冲，要读和写的块也同时被传递给Exec。

• lambda 表达式中使用的所有参数都需要根据以下规则获取：

  • 值捕获: 如果参数变量是一个局部变量，或者将被立刻释放（例如，中间时序）。否 则，一旦foo()存在，这些变量将被销毁。

  • 引用捕获：如果变量是记录在 python 端或者是一个持久变量（例如 Conv2d 类中的 参数 W 和 ConvHand）。

  • 可变捕获: 如果在_foo()中修改了由值捕获的变量，则 lambda 表达式应带有 mutable（可变）标签。

下面是一个在后台实现的操作 的例子：

Tensor GpuConvBackwardx(const Tensor &dy, const Tensor &W, const Tensor &x,
                        const CudnnConvHandle &cch) {
  CHECK_EQ(dy.device()->lang(), kCuda);

  Tensor dx;
  dx.ResetLike(x);

  dy.device()->Exec(
      /*
       * dx is a local variable so it's captured by value
       * dy is an intermediate tensor and isn't recorded on the python side
       * W is an intermediate tensor but it's recorded on the python side
       * chh is a variable and it's recorded on the python side
       */
      [dx, dy, &W, &cch](Context *ctx) mutable {
        Block *wblock = W.block(), *dyblock = dy.block(), *dxblock = dx.block();
        float alpha = 1.f, beta = 0.f;
        cudnnConvolutionBackwardData(
            ctx->cudnn_handle, &alpha, cch.filter_desc, wblock->data(),
            cch.y_desc, dyblock->data(), cch.conv_desc, cch.bp_data_alg,
            cch.workspace.block()->mutable_data(),
            cch.workspace_count * sizeof(float), &beta, cch.x_desc,
            dxblock->mutable_data());
      },
      {dy.block(), W.block()}, {dx.block(), cch.workspace.block()});
      /* the lambda expression reads the blocks of tensor dy and w
       * and writes the blocks of tensor dx and chh.workspace
       */

  return dx;
}

Benchmark

单节点

• 实验设定
  • 模型：
    • 使用层: ResNet50 in resnet.py
    • 使用模型: ResNet50 in resnet.py
  • GPU: NVIDIA RTX 2080Ti
• 注释：
  • s ：second，秒
  • it ： iteration，迭代次数
  • Mem：peak memory usage of single GPU，单 GPU 显存峰值
  • Throughout：number of images processed per second，每秒处理的图像数
  • Time：total time，总时间
  • Speed：iterations per second。每秒迭代次数
  • Reduction：the memory usage reduction rate compared with that using layer，与使用层的内存使用率相比，内存使用率降低了多少
  • Speedup: speedup ratio compared with dev branch，与 dev 分支相比的加速率
• 结果：

  Batchsize	Cases	Mem(MB)	Time(s)	Speed(it/s)	Throughput	Reduction	Speedup
  16	layer	4975	14.1952	14.0893	225.4285	0.00%	1.0000
  	model:disable graph	4995	14.1264	14.1579	226.5261	-0.40%	1.0049
  	model:enable graph, bfs	3283	13.7438	14.5520	232.8318	34.01%	1.0328
  	model:enable graph, serial	3265	13.7420	14.5540	232.8635	34.37%	1.0330
  32	layer	10119	13.4587	7.4302	237.7649	0.00%	1.0000
  	model:disable graph	10109	13.2952	7.5315	240.6875	0.10%	1.0123
  	model:enable graph, bfs	6839	13.1059	7.6302	244.1648	32.41%	1.0269
  	model:enable graph, serial	6845	13.0489	7.6635	245.2312	32.35%	1.0314

多线程

• 实验设置：
  • API：
    • 使用层: ResNet50 in resnet_dist.py
    • 使用模型: ResNet50 in resnet.py
  • GPU: NVIDIA RTX 2080Ti * 2
  • MPI: 在同一节点上的两个 MPI processes
• 注释: 与上面相同
• 结果：

  Batchsize	Cases	Mem(MB)	Time(s)	Speed(it/s)	Throughput	Reduction	Speedup
  16	layer	5439	17.3323	11.5391	369.2522	0.00%	1.0000
  	model:disable graph	5427	17.8232	11.2213	359.0831	0.22%	0.9725
  	model:enable graph, bfs	3389	18.2310	10.9703	351.0504	37.69%	0.9507
  	model:enable graph, serial	3437	17.0389	11.7378	375.6103	36.81%	1.0172
  32	layer	10547	14.8635	6.7279	430.5858	0.00%	1.0000
  	model:disable graph	10503	14.7746	6.7684	433.1748	0.42%	1.0060
  	model:enable graph, bfs	6935	14.8553	6.7316	430.8231	34.25%	1.0006
  	model:enable graph, serial	7027	14.3271	6.9798	446.7074	33.37%	1.0374

结论

• 在启用计算图的情况下进行训练，可以显著减少内存占用。
• 目前，在速度上有一点改进。在效率方面还可以做更多的优化。