Model
The forward and backward propagation in a neural network can be represented using a set of operations such as convolution and pooling. Each operation takes some input tensors and applies an operator to generate output tensors. By representing each operator as a node and each tensor as an edge, all operations form a computational graph. With the computational graph, speed and memory optimization can be conducted by scheduling the execution of the operations and memory allocation/release intelligently. In SINGA, users only need to define the neural network model using the Model API. The graph is constructed and optimized at the C++ backend automatically.
In this way, on the one hand, users implement a network using the Model API following the imperative programming style like PyTorch. Different from PyTorch which recreates the operations in every iteration, SINGA buffers the operations to create a computational graph implicitly (when this feature is enabled) after the first iteration. Therefore, on the other hand, SINGA has a similar computational graph as the one created by libraries using declarative programming, e.g., TensorFlow. Consequently, it can enjoy the optimizations done over the graph.
Example
The following code illustrates the usage of the Model API.
- Implement the new model as a subclass of the Model class.
class CNN(model.Model):
def __init__(self, num_classes=10, num_channels=1):
super(CNN, self).__init__()
self.conv1 = layer.Conv2d(num_channels, 20, 5, padding=0, activation="RELU")
self.conv2 = layer.Conv2d(20, 50, 5, padding=0, activation="RELU")
self.linear1 = layer.Linear(500)
self.linear2 = layer.Linear(num_classes)
self.pooling1 = layer.MaxPool2d(2, 2, padding=0)
self.pooling2 = layer.MaxPool2d(2, 2, padding=0)
self.relu = layer.ReLU()
self.flatten = layer.Flatten()
self.softmax_cross_entropy = layer.SoftMaxCrossEntropy()
def forward(self, x):
y = self.conv1(x)
y = self.pooling1(y)
y = self.conv2(y)
y = self.pooling2(y)
y = self.flatten(y)
y = self.linear1(y)
y = self.relu(y)
y = self.linear2(y)
return y
def train_one_batch(self, x, y):
out = self.forward(x)
loss = self.softmax_cross_entropy(out, y)
self.optimizer(loss)
return out, loss
- Create an instance of model, optimizer, device, etc. Compile the model
model = CNN()
# initialize optimizer and attach it to the model
sgd = opt.SGD(lr=0.005, momentum=0.9, weight_decay=1e-5)
model.set_optimizer(sgd)
# initialize device
dev = device.create_cuda_gpu()
# input and target placeholders for the model
tx = tensor.Tensor((batch_size, 1, IMG_SIZE, IMG_SIZE), dev, tensor.float32)
ty = tensor.Tensor((batch_size, num_classes), dev, tensor.int32)
# compile the model before training
model.compile([tx], is_train=True, use_graph=True, sequential=False)
- Train the model iteratively
for b in range(num_train_batch):
# generate the next mini-batch
x, y = ...
# Copy the data into input tensors
tx.copy_from_numpy(x)
ty.copy_from_numpy(y)
# Training with one batch
out, loss = model(tx, ty)
A Google Colab notebook of this example is available here.
More examples:
Implementation
Graph Construction
SINGA constructs the computational graph in three steps:
- buffer the operations
- analyze the dependencies operations
- create the nodes and edges based on the dependencies
Take the matrix multiplication operation from the dense layer of a
MLP model
as an example. The operation is called in the forward function of the MLP
class
class MLP(model.Model):
def __init__(self, data_size=10, perceptron_size=100, num_classes=10):
super(MLP, self).__init__()
self.linear1 = layer.Linear(perceptron_size)
...
def forward(self, inputs):
y = self.linear1(inputs)
...
The Linear layer is composed of the mutmul operator. autograd implements
the matmul operator by calling the function Mult exposed from CPP via SWIG.
# implementation of matmul()
singa.Mult(inputs, w)
At the backend, the Mult function is implemented by calling GEMV a CBLAS
function. Instead of calling GEMV directly, Mult submits GEMV and the
arguments to the device as follows,
// implementation of Mult()
C->device()->Exec(
[a, A, b, B, CRef](Context *ctx) mutable {
GEMV<DType, Lang>(a, A, B, b, &CRef, ctx);
},
read_blocks, {C->block()});
The Exec function of Device buffers the function and its arguments. In
addition, it also has the information about the blocks (a block is a chunk of
memory for a tensor) to be read and written by this function.
Once Model.forward() has been executed once, all operations are buffered by
Device. Next, the read/write information of all operations are analyzed to
create the computational graph. For example, if a block b is written by one
operation O1 and is later read by another operation O2, we would know O2 depends
on O1 and there is a directed edge from A to B, which represents block b (or
its tensor). After that a directed acyclic graph is constructed as shown below.
The graph is constructed once.
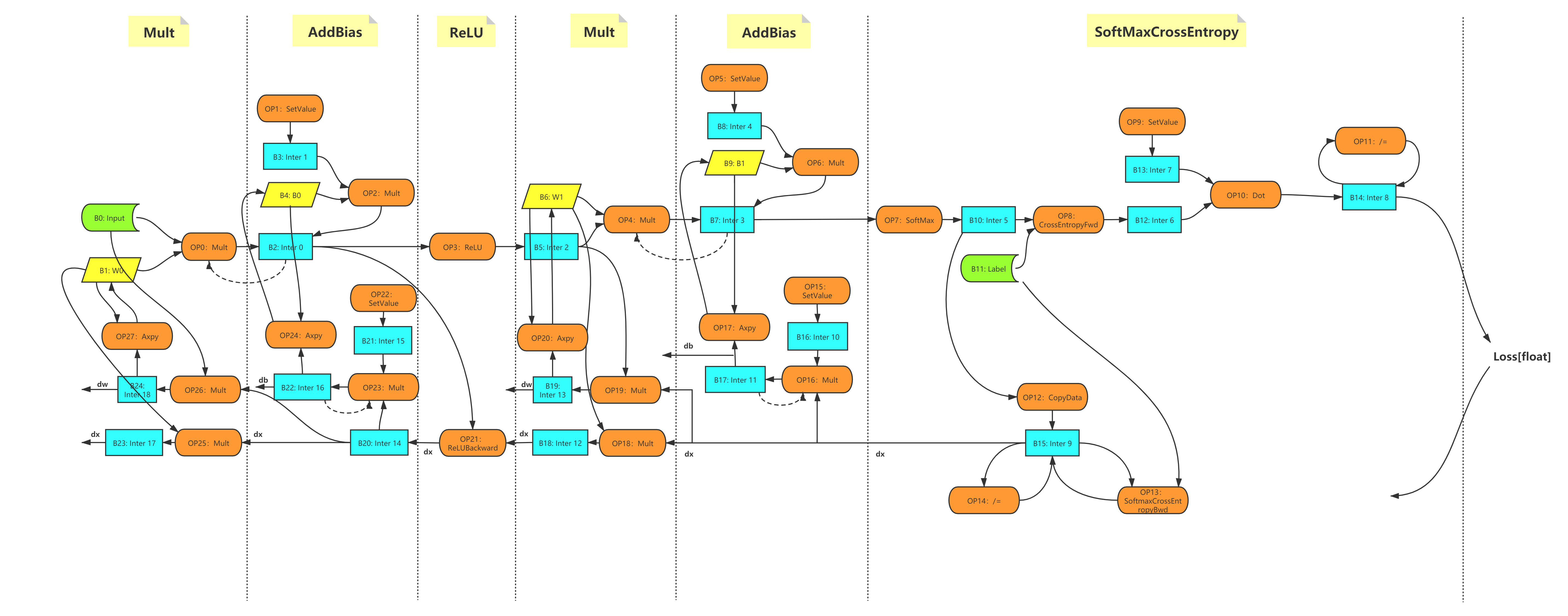
Figure 1 - The computational graph of the MLP example.
Optimization
Currently, the following optimizations are done based on the computational graph.
Lazy allocation When tensor/blocks are created, devices do not allocate memory for them immediately. Instead, when the block is accessed for the first time, the memory is allocated.
Automatic recycling The reference count of each tensor/block is calculated based on the graph. Before executing the operations, the reference count is the number of operations that read this block. During the execution, once an operation is executed, the reference count of the every input block is decreased by 1. If one block's reference count reaches 0, it means that this block will not be read again in the remaining operations. Therefore, its memory can be released safely. In addition, SINGA tracks the usage of the block outside of the graph. If a block is used by Python code (not by autograd operators), it will not be recycled.
Memory sharing SINGA uses memory pool, e.g.,
CnMem to manage CUDA memory. With Automatic
recycling and memory pool, SINGA can share the memory among tensors. Consider
two operations c = a + b and d=2xc. Before executing the second operation,
according to Lazy allocation, the memory of d should be allocated. Suppose a
is not used in the rest operations. According to Automatic recycling, the block
of a will be released after the first operation. Therefore, SINGA would submit
four operations to the CUDA stream: addition, free a, malloc b, and
multiplication. The memory pool is then able to share the memory released by a
with b instead of ask the GPU to do real malloc for b.
Other optimization techniques e.g., from compliers, such as common sub-expression elimination and parallelizing operations on different CUDA streams can also be applied.
New Operator
Each operator defined in autograd module implements two functions: forward and
backward, which are implemented by calling the operators from the backend. To
add a new operator in autograd, you need to add the multiple operators at the
backend.
Take the Conv2d operator as an example, at the Python side, the forward and backward function are implemented by calling the operators from the backend depending on the device type.
class _Conv2d(Operation):
def forward(self, x, W, b=None):
......
if training:
if self.handle.bias_term:
self.inputs = (x, W, b) # record x, W, b
else:
self.inputs = (x, W)
if (type(self.handle) != singa.ConvHandle):
return singa.GpuConvForward(x, W, b, self.handle)
else:
return singa.CpuConvForward(x, W, b, self.handle)
def backward(self, dy):
if (type(self.handle) != singa.ConvHandle):
dx = singa.GpuConvBackwardx(dy, self.inputs[1], self.inputs[0],
self.handle)
dW = singa.GpuConvBackwardW(dy, self.inputs[0], self.inputs[1],
self.handle)
db = singa.GpuConvBackwardb(
dy, self.inputs[2],
self.handle) if self.handle.bias_term else None
else:
dx = singa.CpuConvBackwardx(dy, self.inputs[1], self.inputs[0],
self.handle)
dW = singa.CpuConvBackwardW(dy, self.inputs[0], self.inputs[1],
self.handle)
db = singa.CpuConvBackwardb(
dy, self.inputs[2],
self.handle) if self.handle.bias_term else None
if db:
return dx, dW, db
else:
return dx, dW
For each operator at the backend, it should be implemented in the following way:
Suppose the operator is
foo(); its real implementation should be wrapped in another function e.g.,_foo().foo()passes_footogether with the arguments as a lambda function toDevice'sExecfunction for buffering. The blocks to be read and written are also passed toExec.All arguments used in the lambda expression need to be captured according to the following rules.
capture by value: If the argument variable is a local variable or will be immediately released (e.g. intermediate tensors). Otherwise, these variables will be destroyed oncefoo()exists.capture by reference:If the variable is recorded on the python side or a persistent variable (e.g. parameter W and ConvHand in the Conv2d class).mutable: The lambda expression should have the mutable tag if a variable captured by value is modified in_foo()
Here is one example operator implemented at the backend.
Tensor GpuConvBackwardx(const Tensor &dy, const Tensor &W, const Tensor &x,
const CudnnConvHandle &cch) {
CHECK_EQ(dy.device()->lang(), kCuda);
Tensor dx;
dx.ResetLike(x);
dy.device()->Exec(
/*
* dx is a local variable so it's captured by value
* dy is an intermediate tensor and isn't recorded on the python side
* W is an intermediate tensor but it's recorded on the python side
* chh is a variable and it's recorded on the python side
*/
[dx, dy, &W, &cch](Context *ctx) mutable {
Block *wblock = W.block(), *dyblock = dy.block(), *dxblock = dx.block();
float alpha = 1.f, beta = 0.f;
cudnnConvolutionBackwardData(
ctx->cudnn_handle, &alpha, cch.filter_desc, wblock->data(),
cch.y_desc, dyblock->data(), cch.conv_desc, cch.bp_data_alg,
cch.workspace.block()->mutable_data(),
cch.workspace_count * sizeof(float), &beta, cch.x_desc,
dxblock->mutable_data());
},
{dy.block(), W.block()}, {dx.block(), cch.workspace.block()});
/* the lambda expression reads the blocks of tensor dy and w
* and writes the blocks of tensor dx and chh.workspace
*/
return dx;
}
Benchmark
Single node
- Experiment settings
- Notations
s:secondit: iterationMem:peak memory usage of single GPUThroughout:number of images processed per secondTime:total timeSpeed:iterations per secondReduction:the memory usage reduction rate compared with that using layerSpeedup: speedup ratio compared with dev branch
- Result
Batchsize Cases Mem(MB) Time(s) Speed(it/s) Throughput Reduction Speedup 16 layer 4975 14.1952 14.0893 225.4285 0.00% 1.0000 model:disable graph 4995 14.1264 14.1579 226.5261 -0.40% 1.0049 model:enable graph, bfs 3283 13.7438 14.5520 232.8318 34.01% 1.0328 model:enable graph, serial 3265 13.7420 14.5540 232.8635 34.37% 1.0330 32 layer 10119 13.4587 7.4302 237.7649 0.00% 1.0000 model:disable graph 10109 13.2952 7.5315 240.6875 0.10% 1.0123 model:enable graph, bfs 6839 13.1059 7.6302 244.1648 32.41% 1.0269 model:enable graph, serial 6845 13.0489 7.6635 245.2312 32.35% 1.0314
Multi processes
- Experiment settings
- API
- using Layer: ResNet50 in resnet_dist.py
- using Model: ResNet50 in resnet.py
- GPU: NVIDIA RTX 2080Ti * 2
- MPI: two MPI processes on one node
- API
- Notations: the same as above
- Result
Batchsize Cases Mem(MB) Time(s) Speed(it/s) Throughput Reduction Speedup 16 layer 5439 17.3323 11.5391 369.2522 0.00% 1.0000 model:disable graph 5427 17.8232 11.2213 359.0831 0.22% 0.9725 model:enable graph, bfs 3389 18.2310 10.9703 351.0504 37.69% 0.9507 model:enable graph, serial 3437 17.0389 11.7378 375.6103 36.81% 1.0172 32 layer 10547 14.8635 6.7279 430.5858 0.00% 1.0000 model:disable graph 10503 14.7746 6.7684 433.1748 0.42% 1.0060 model:enable graph, bfs 6935 14.8553 6.7316 430.8231 34.25% 1.0006 model:enable graph, serial 7027 14.3271 6.9798 446.7074 33.37% 1.0374
Conclusion
- Training with the computational graph enabled can significantly reduce the memory footprint.
- Currently, there is a little improvement in terms of speed. More optimizations can be done towards the efficiency.
